X-12-ARIMA 入門
X-12-ARIMA使用についての手順概略
・60データ以上を準備。
・ARIMAで使用できるようにデータファイルを変換する。
・指定のデータの並びに変換して、textファイルで保存。
・ARIMAのスペックファイルを作成する。スペックファイルは拡張子が".spc"となっているファイル。テキストファイル作成と同様の手順で、最後に拡張子を変える。
・ARIMAモデルの決定や外れ値の抽出、回帰変数の採用など演算プログラムを決定する。
・スペックファイルの内容によって、季節調整データが変化する。
4. "実行"し出力する
・ARIMAの"実行ファイル"で、作成したスペックファイルを指定し演算を実行する。
・季節調整データを出力し、そのデータを使用する。
・少なくとも60データ(月データ:5年分、期データ:15年分)を準備
・エクセル等にて、縦1列、または縦=年・横=月(または期)の並びでデータを整理する。
※各データのみを記入。年月は記入しないこと。
※各データは3桁を越える場合にコンマで区切らないこと。ただし、小数点は可。
((例)12,345:不可 → 12345:可)
・テキストファイルで保存。 ※1ファイルに1時系列しか記載できない。
・ARIMAは日本語を認識ぜずエラーが起こる原因となるため、保存先は全て英数字表記のフォルダにしなければならない。
(例)
縦1列 表記の場合
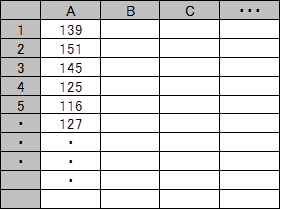
縦に年、横に月で表記する場合(横は最大12データ(12ヶ月分)になる)
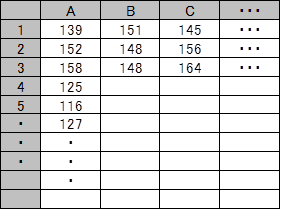
■スペックファイルとは・・・x-12-ARIMAを実行するプログラムファイル。
※X11defaultを実行する場合にも作成は必要。
~スペックファイル作成の手順概略~
![]()
(3)回帰変数の策定。
![]()
・階差の決定。
・自己相関、偏自己相関の影響を除去するための変数の設定。
![]()
![]()
・ここで季節調整データの出力を指定する。
・x11defaultを使用する場合は、②から⑤までの手順は省略。
![]()
スペックファイルの完成
※スペックファイルは、完成までに各手順を踏む際に書き換えることとなるが、一連の演算においては上書きで構わない。
~スペックファイルの書き方(基本)~
・スペックファイルは、textファイルで作成して".spc"の拡張子を名前の最後につける。
※自動的にアイコンは変化する。

(内容の基本ルール)
・スペックファイルでは、"コマンド"により各種設定の指示を行う。
・一つのコマンドについて、コマンド、かっこ、詳細指示コマンドのスタイルをとり、各コマンドの設定が終わる毎に改行し次のコマンド指示を行う。
[各指示コマンド基本書式]
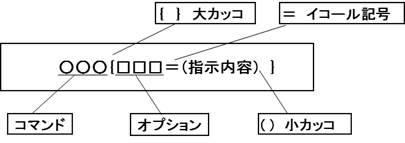
[基本的なコマンドと各コマンドの基本表記方法]
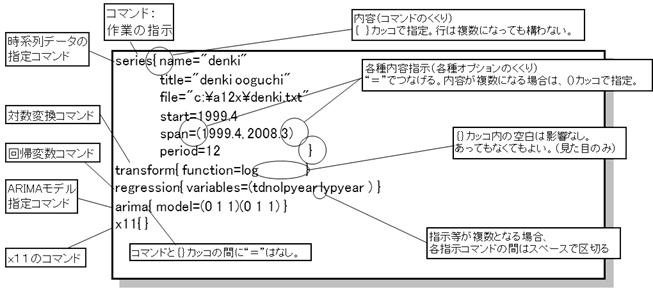
3-(1) 対象となる時系列データの指定 『series』コマンド
・seriesコマンド:時系列データファイルとデータファイルの開始時期を指定する。
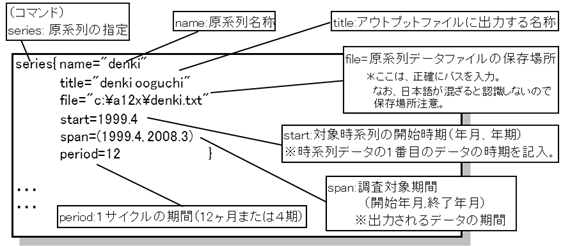
・x-12-ARIMAは、月次データまたは四半期データを対象とすることができる。
月次データの場合 ⇒ period=12
四半期データの場合 ⇒ period=4
注意点として、月次データの場合は、startおよびspanの記入が" yyyy(年).mm(月)"となるのに対し(m=1~12)、四半期データの場合は、" yyyy(年).q(期)"(q =1~4)となることに留意すること。
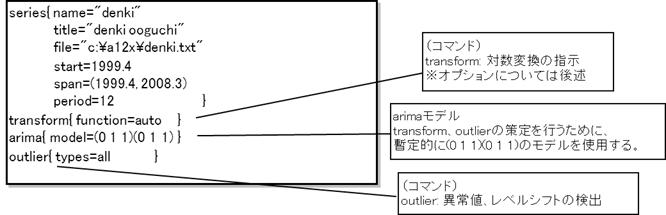

上記のスペックファイルでx12ARIMAを実行すると、スペックファイルと同じフォルダに結果ファイルが出力され、その内、" ***.out"ファイルに評価が記載されている。
【下記のような出力がされた場合】
(対数変換について)
(パターン1)
![]()
→対数変換を行うことを勧める。(乗法型) → transform{ function=log }を採用する。
(パターン2)
![]()
→対数変換を行うことを勧めない。(加法型)→ transform{ function }を採用しない。
(外れ値の検出について)
(パターン1)

→異常値やレベルシフトは検出されなかった。
(パターン2)
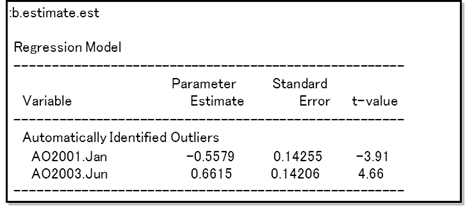
→2001.1と2003.6のデータが異常であると判断された。
→後に、変数コマンド(regression)にて抽出された外れ値を処理して演算を行う。
※外れ値の自動探索では、目で見る限り判明しないようなレベルシフトの存在を示唆する場合もあるので、レベルシフトの発生原因があまり明白でないものに関しては、安定性の観点から、レベルシフトとして取り入れるかどうか十分考慮する必要がある。
※一方で、異常値については、X-11による移動平均処理時の他の時期への影響を回避するために、全ての異常値を取り入れることが望ましい。
※AIC値とは、モデルのあてはまり度とパラメータ数を基に算定される値で、最も小さい値のモデルを選択する。
※outlierコマンドを使用した場合は、AIC値は意味をなさない。したがって、 outlierコマンドで探索された異常値・レベルシフトをモデルに取り入れるかの判断は自ら行い、特にレベルシフトについては、1つずつ発生原因を調査した上で、取り入れるかの判断を行うこと。
*****≪ 補 足 ≫*****
【transformのオプションコマンド】
(表記方法)
![]()
・function:対数変換を行うかどうかの内容指示
(***に入るコマンド)
Auto ・・・対数変換を行った場合と行わなかった場合の2つの評価を行い、結果がより安定するほうを採用する。
Log ・・・対数変換を行う。(乗法型) ※加法型の場合は、このコマンドを指定しない。
※transformコマンドには、オプションコマンドとしてadjustなどもあるが別の手順となるためここでは説明しない。
【outlierのオプションコマンド】
(表記方法)
![]()
(出力の記号と意味)
aoyyyy.mm :異常値(yyyy年、mm月)
lsyyyy.mm :レベルシフト(yyyy年、mm月)
tsyyyy.mm :一時的異常(yyyy年、mm月)
3-(3) 回帰変数の策定 『regression』コマンド
・regressionコマンド:回帰変数を指定するコマンド。様々なオプションコマンドがあり、最も適当であると考えられる回帰変数を採用する。
~回帰変数を自動検索する場合(aictestオプションを利用する)~
・aictestオプション:指定した回帰変数について、回帰変数を利用した場合と利用しなかった場合の AIC値を比較して、最適な回帰変数を評価するオプション。
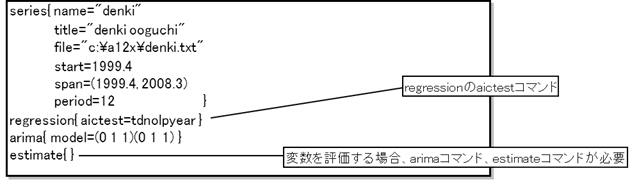
【aictestオプションで判定できる変数】
![]() ・td・・・月の長さと曜日の調整を同時に行う。
・td・・・月の長さと曜日の調整を同時に行う。
・tdnolpyear・・・曜日調整。各曜日の影響。
・tdstock・・・末残ベースのストック系列の曜日調整
・td1coef・・・曜日調整と閏年調整。Td1nolpyearと lpyearを併用した場合と同様。
・td1nolpyear・・・曜日調整。平日と週末の影響。
・user・・・ユーザーファイルを使用。(ジャパンホリデーなど。)
※各オプションは併用できないコマンドがあるので注意。
![]() ・td → td1coef、td1nolpyear、lpyear、 lom、loq、tdstockと併用できない。
・td → td1coef、td1nolpyear、lpyear、 lom、loq、tdstockと併用できない。
・tdnolpyear → td、td1coef、td1nolpyear、 tdstockと併用できない。
・td1coef → td、tdnolpyear、td1nolpyear、 lpyear、lom、loq、tdstockと併用できない。
・td1nolpyear → td、tdnolyear、td1coef、 tdstockと併用できない。
・lpyear → td、td1coef、tdstockと併用できない。
・lom → td、td1coef、tdstockと併用できない。
・tdstock → td、tdnolpyear、td1coef、 td1nolpyear、lom、loqと併用できない。
【aictestオプションにてユーザーファイルを指定する場合の表記方法】

■以上のように、AIC値により判定した回帰変数を採用する。
■併用できないオプションを同時に推奨された場合、出力ファイルのAIC値を参考にして、最も小さい値(安定した値)をとっている変数を採用する。
(例)
【下記のような出力がされた場合】
(パターン1)
![]()
→tdnolpyearを推奨する。
(パターン2)
![]()
→ユーザーファイルの変数を推奨しない。
~回帰変数を独自に判定して採用する場合(aictestオプションを利用しない場合)~
■どのタイプの回帰変数を導入するかは、国の例を参考にするなどして判断する。
■曜日や閏年などの影響が明らかに考えられる場合は、各種変数を代入して演算を行い、結果をみて判断する。
(表記方法)
![]()
【対数変換を行い、かつ月の長さ調整、曜日調整を行いたい場合】
・transform{ adjust=lom }とregression{ variables=tdnolpyear }を使用。原系列を対数変換させる場合のみ有効。
※transformのadjustオプションは、事前調整を行うコマンドであり、変数の指定と同様の影響がある。
(パターン1)
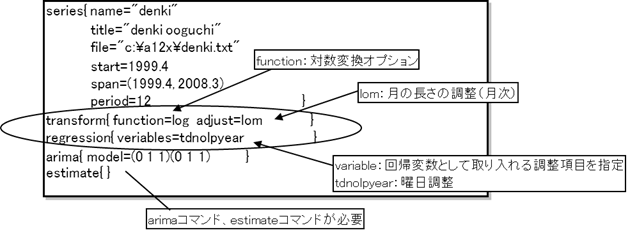
(パターン2)
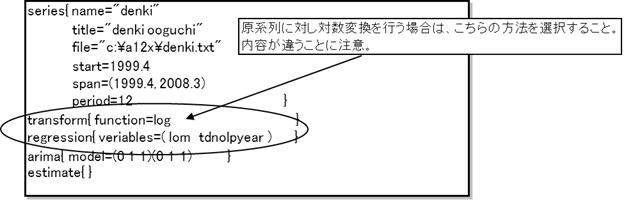
(パターン3)
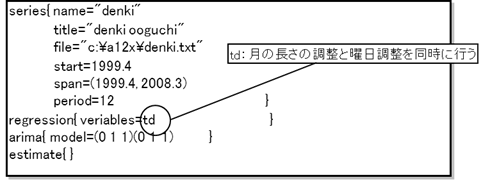
※各スペックファイルの様式は、併用するオプションなどを考慮し工夫すること。
【閏年調整および曜日調整を行いたい場合】
・transform{ function=log }とregression{ variables=td }を使用する。原系列を対数変換する場合のみ有効。
(パターン1)
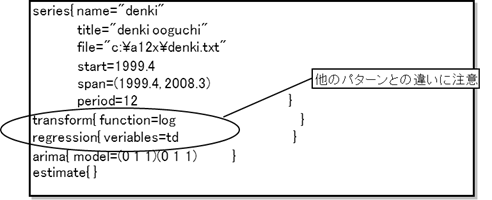
(パターン2)
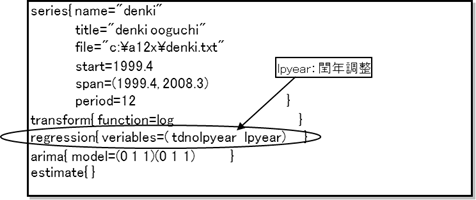
【フロー系列および平残ベースのストック系列の場合・・・ regression{ variables=tdnolpyear }】
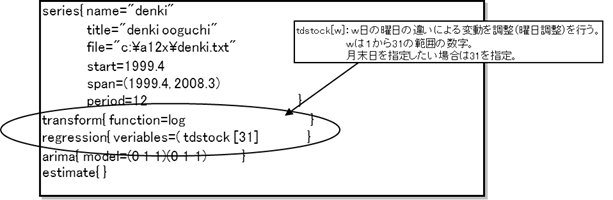
【末残ベースのストック系列の場合・・・ regression{ variables=( tdstock [w] )} 】
■他にも適用したい変数がある場合は、独自で工夫して採用すればよい。結果については、AIC値が最も小さい値(安定した値)を示した変数が最も適していると考えられる。
~その他(特殊な設定を行いたい場合)~
■対象期間内で曜日構成が変化するケースの場合、変化前と変化後に期間を分けて各種の調整を行う。
■regressionコマンドにて、variablesオプションを用いて{調整項目 /yyyy.mm/}(yyyy:年、mm:月)で期間を分割して回帰する。
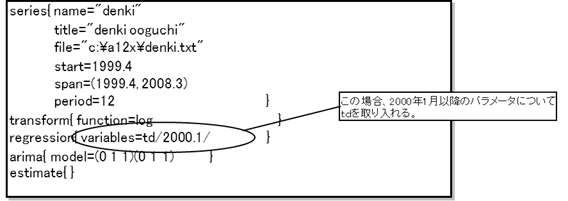
■期間を分割したほうがよいかどうかは、分割したモデルと分割しないモデルのAIC値を比較する。
■確定的なトレンドが見て取れた場合、モデルへの定数項の取り込みができる。対数変換後の時系列が確定的なトレンドを持つならば、階差処理後の時系列を定数項つきのモデルであらわすことができる。
■定数項をモデルに取り入れるべきかが不明な場合は、まず「regression」コマンドに定数項( "const")を指定し、モデルの推計を行う。推計された定数項のパラメータが有意でない場合は、モデルに取り入れる必要はない。また、 AIC値を比較し、AIC値が小さいほうを採用する。
(例)
(スペックファイル)
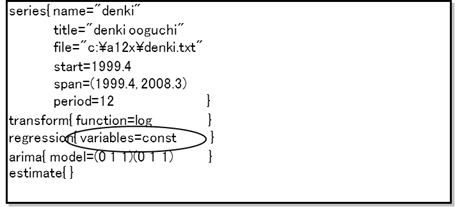
(出力)

■パラメータの有意性はt値をもとに判定する。
*****≪ 補 足 ≫*****
【regressionコマンドの各オプション】
・曜日調整に係るオプションコマンド
td :月の長さと曜日の調整を同時に行う。
td1coef :曜日調整と閏年調整。Td1nolpyearとlpyearを併用した場合と同様。
tdnolpyear :曜日調整。各曜日の影響。
td1nolpyear :曜日調整。平日と週末の影響。
・閏年調整、月の長さ調整に係るオプションコマンド
lpyear :閏年調整
lom :月の長さ調整
td1coef :曜日調整と閏年調整。Td1nolpyearとlpyearを併用した場合と同様。
td :月の長さと曜日の調整を同時に行う。
・その他のオプションコマンド
loq :四半期の長さの調整
user :ユーザーファイルの使用(ユーザーオプションの適用)
tdstock :月の末日の曜日の違いによって引き起こされる変動を調整。
ao、ls、tc:各種外れ値の抽出
【ユーザー変数のデータファイルの作成について】
(1)textファイルで作成して".dat"または".txt"の拡張子を名前の最後につける。
(2)原系列データと同様に、各時期の変数データを縦に時系列に並べる。
(例)勤務日の日数に影響されるデータを季節調整する場合、近年は週休2日が完全に定着しているので、最近のデータのみを扱う場合には、作成方法1による方がいい結果がでると考えられる。作成方法1の場合、曜日調整には td1nolpyear 又は td1coef を使用する。
・日本型曜日調整例:作成方法1
①実際のカレンダーより、下記条件の日数を抽出。(休日数をカウントする。)
(条件)
○月~金曜日が祝日となっている日数(カレンダー要因のみを取り入れた場合)
○必要に応じて、以下のルールで休日を追加する。
年始休業:1月1~3日を休日とする。
ゴールデンウィーク:4月29日~5月 5日の間は、中2日以内のウィークデイを休日とする。
お盆休み:8月13日~15日を休日とする。
年末休業:12月29日~31日を休日とする。
②X-12-ARIMA対応変数として、各月毎に【 各データ - 全データの平均値 】とし、各月データを時系列に整理する。
(例)
9月 / 全期間平均値 2.0
|
|
月間休日数 |
計算式 |
x-12-ARIMA対応変数 |
|
2008年9月 |
1 | 1 - 2.0 = | -1.0 |
|
2009年9月 |
3 |
3 - 2.0 = |
1.0 |
|
2010年9月 |
2 |
2 - 2.0 = |
0.0 |
|
2011年9月 |
2 |
2 - 2.0 = |
0.0 |
・日本型曜日調整例:作成方法2
①実際のカレンダーより、下記条件の日数を抽出。(休日数をカウントする。)
(条件)
○月~土曜日が祝日または休日となっている日数(カレンダー要因のみを取り入れた場合)
○土曜日については、1992年4までは月に2回休日(第 2、第4土曜日)、1992年5月以降は全ての土曜日を休日とする。
○必要に応じて、以下のルールで休日を追加する。年始休業:1月1~3日を休日とする。
ゴールデンウィーク:4月29日~5月 5日の間は、中2日以内のウィークデイを休日とする。
お盆休み:8月13日~15日を休日とする。
年末休業:12月29日~31日を休日とする。
②X-12-ARIMA対応変数として、【 各データ - 全データの平均値 】とし、各時期データを時系列に整理する。
(例)
1997年10月~12月 / 全期間平均値 5.127
|
|
月間休日数 |
計算式 |
x-12-ARIMA対応変数 |
|
1997年10月 |
5 |
5 - 5.127 = |
-0.127 |
|
11月 |
7 |
7 - 5.128 = |
1.873 |
|
12月 |
8 |
8 - 5.129 = |
2.873 |
参考資料)
奥本佳伸、2001年6月、千葉大学経済研究大16巻 1号、「季節調整法センサス局法X-12-ARIMAの適用における日本型曜日調整の有効性」、 p.239-281
3-(4) ARIMAモデルの決定 『automdl』『 idetify』『 arima』コマンド
■ARIMAモデルについては、≪参考≫ARIMAモデルについてで説明。
X-12-Arima の Ver 3 では、TRAMO の自動モデル選択機能が導入されているので、それを使うと簡単に最適なARIMAモデルを選択することができるようになっている。使用方法は、スペックファイルで、reregression コマンドの下に arima コマンドや identyfy コマンドの代わりに、次のとおり automdl コマンドを記述する。
automdl { }
automdl は、上のように引数を指定しなくても、既定の設定で動作する。引数の詳細については、X-12-ARIMA Reference Manual の 7.2 AUTOMDL を参照のこと。また、日本語の参考資料としては、以下の文献を参照。
奥本佳伸、2001年6月、千葉大学経済研究第24巻3・4号、「季節調整法プログラムセンサス局法 X-12-ARIMAのversion 0.3について」
以下は、従来の方法を説明したものである。手間はかかるものの ARIMA モデルについての理解を深めることはできる。
1)これまでに決定した回帰変数、外れ値を採用したうえで、階差の判定を行う。
・identifyコマンド:階差の判定。
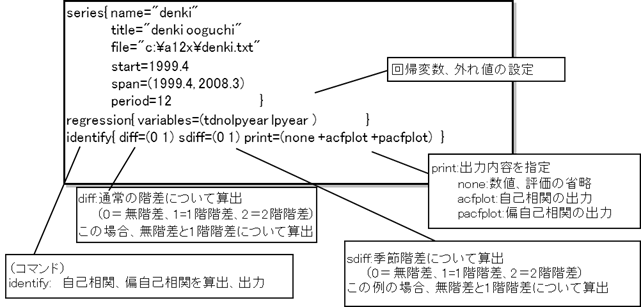
■階差をとるべきかの判断をする。出力されるグラフから、最も相関がない条件を選ぶ。
(グラフからの判断基準)
・12、24、36(月次データの場合)や 4、8、12(四半期データの場合)の次数のプロットにおいて有意な相関が発生しており、プロットの高次次数へ向けての動きが滑らか
→ 季節階差をとる必要あり。
・高次の次数においても有意な相関が発生しており、プロットの高次次数へむけての動きが滑らか
→ 通常の階差をとる必要あり。
・全体に有意な相関がなくなり、プロットの動きも滑らかでないとき(ただし、いくつかの次数においては有意な相関がみられることもある)
→ 階差をとる必要なし。
・1階の階差の自己相関プロットをみてさらに階差をとる必要がある場合は、階差を2階とる。また、自己相関のプロットから判断しにくい場合は、原系列、 1階階差の系列のプロットからトレンドが除去されているかの確認をする。
(出力グラフの見方)
■".out"ファイルにて出力される。
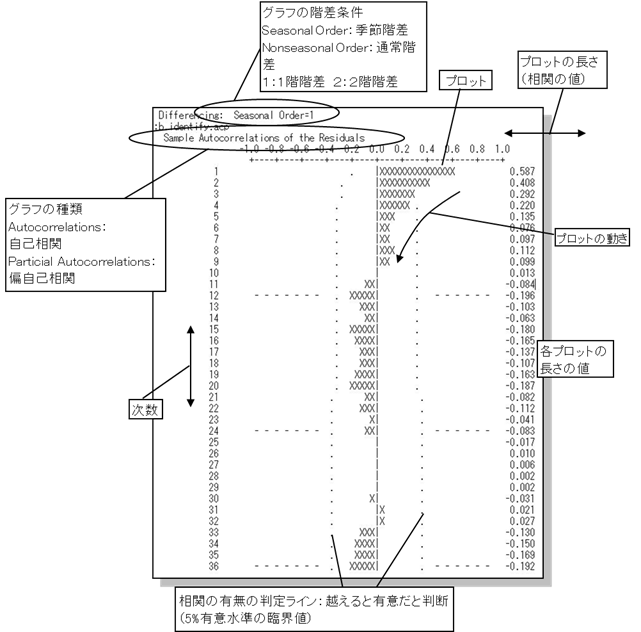
(例)
自己相関プロット
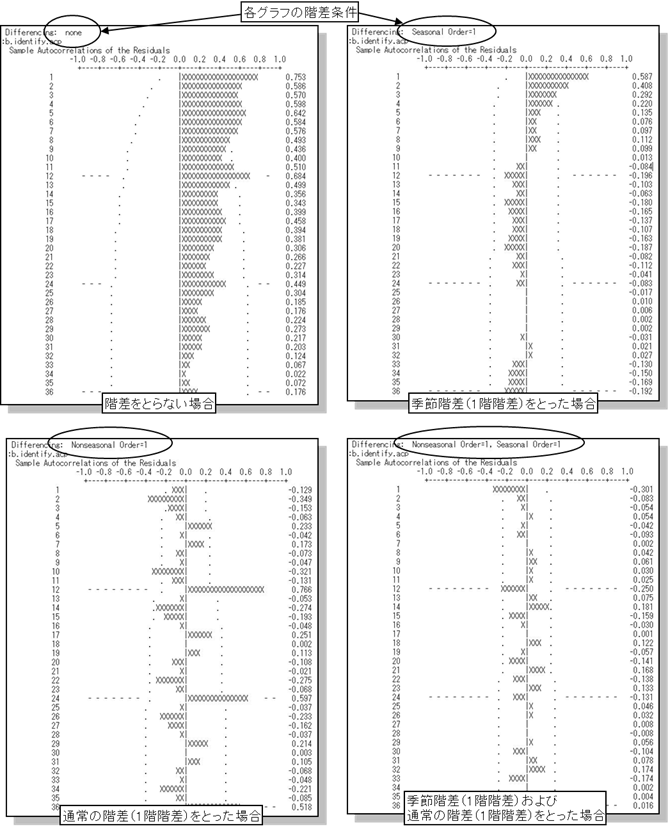
・以上の4パターンのグラフから判断して、季節階差および通常の階差の両方をとると判断する。 (相関の有無について判断する。)
また、両方の1階階差をとった時点で全体にほとんど有意な相関がみられなくなったため、これ以上の階差は不要と判断。
※ARIMAモデルにおいて、通常の階差:d、季節階差:Dと表す。この場合、 d=1、D=1 となる。
2)ARIMAモデル( ARIMA(p d q)(P D Q) )を作成する。
・arimaコマンド:arimaモデルの判定。
■階差を判断したプロット図を利用して、ARIMAモデルの候補を作成する。使用するプロット図は、決定した階差の自己相関、偏自己相関を使う。(上記サンプルでは、 d=1、D=1の相関図について)
■季節階差をとった場合、ARIMA(P D Q)について、ARモデル、MAモデル、ARMAモデルのいずれが当てはまるかを判断する。判断方法の詳細は別紙説明。
■通常の階差をとった場合、ARIMA(p d q)について、ARモデル、MAモデル、ARMAモデルのいずれが当てはまるかを判断する。判断方法の詳細は別紙説明。
■下記のようなスペックファイルを作成して各ARIMAモデルの候補を推計し、最適なARIMAモデルを決定する。 ※数パターンの ARIMAモデル候補を試す。
(ARIMAモデル推計のためのスペックファイル(ARIMAモデル推計のプログラム))
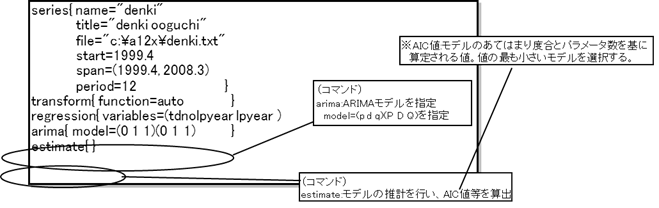
(例)
d=1,D=1のグラフ(プロット図)からの判断により(1,1,1)(0,1,1)、 (1,1,1)(1,1,1)、(1,1,0)(1,1,1)、(1,10)(1,1,2)のいずれかのモデルが当てはまるであろうと推測し、各モデルについて ARIMAモデルの推計を行う。
(出力結果例)
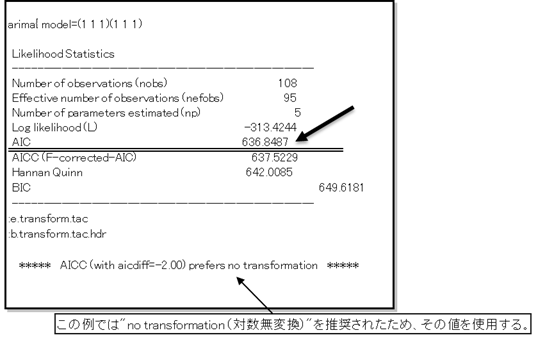
上図のように、AIC値が表示される。この場合、ARIMA(1,1,1)(1,1,1)において AIC値は636.8487を示している。
また同様に他のモデルを試したところ、
|
ARIMAモデル |
AIC値 |
|
(1 1 1)(0 1 1) |
635.4451 |
|
(1 1 1)(1 1 1) |
636.8487 |
|
(1 1 0)(1 1 1) |
643.4968 |
|
(1 1 0)(1 1 2) |
645.1287 |
という結果になったため、今回は(1,1,1)(0,1,1)を最適モデルとして選択する。
(注意)実際の手順として様々なパラメータを代入し、AIC値を比較して ARIMAモデルを決定するが、異なる階差(d、D)のパラメータ同士を比較することはできない。したがって、階差は事前に決定しなければいけない。(階差が大きいほど、自動的に AIC値は小さくなる。)
■選択したモデルについて、念のため各パラメータの有意性の確認を行うことが望ましい。各パラメータのt値を求め、有意でない場合はモデルの次数を変更する。(最適モデルでない可能性を示唆。)
【計算式】t値=(Estimate)/(StandardErrors)
○各数値は同推計結果にて表示され、t値は手計算。t値が2以上であれば有意。
(例)
有意性のチェック

ARIMA(1,1,1)(1,1,1)について推計したところ、Estimateおよび StandardErroesについて上図のような結果がでた。
この場合、Seasonal AR Lag12において0.137/0.13853=0.9889<2となったため、季節 ARIMA(P値)について次数を変更するべき可能性を示唆されている。
結果、ARIMA(1,1,1)(0,1,1)のほうがよりAIC値が低く最適であると判断された。
ARIMA(1,1,1)(0,1,1)についてt値を求めるとすべてのパラメータにおいてt=2以上の値を示したため有意と判断された。
■ここまでの手順で判定された異常値や変数、ARIMAモデルを設定する。
(例)
(スペックファイルの書き方)
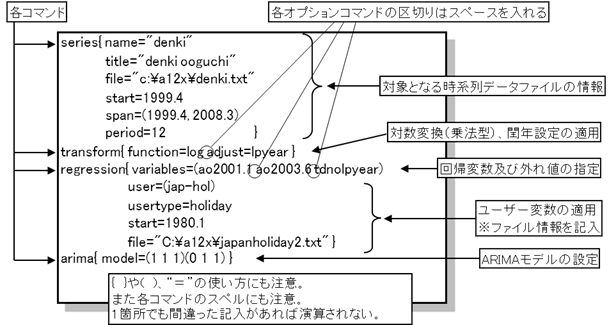
~予測値の推計~
■ARIMAモデルを用いて、4~5年分の予測値を推計する。
・forecastコマンド、maxleadオプション…予測する期数を指定(デフォルトは月次データの場合 12期、四半期データの場合4期。最高60期まで指定可能)。
※forecastコマンドを指定しない場合でも、REGARIMAモデルを指定した場合は、自動的に 1年分の予測値が推計される。予測値の推計を行わない場合は、maxleadオプションに0を指定する。

3-(6) x-11ARIMAの実行プログラムを設定する。 『 x11』コマンド
・X11コマンド・・・
mode オプション:乗法型または加法型のモデルを選択。乗法型の場合は省略しても構わないが、加法型の場合は必ず mode=add を指定すること。
appendfcst オプション:セーブファイルへ出力する事前調整済系列、曜日変動成分および季節変動成分にforecastコマンドで作成した予測値を追加するかの指定( yes:追加する no:追加しない)
save オプション:セーブファイルへ出力するテーブル名を指定(「テーブル名」:下記にて別途説明)
■X-11には、いくつかのオプションがある(下記にて別途説明)。 季節調整を適用する時系列データの性格に合わせて適当なオプション値を選ぶことで、よりよい季節調整結果が得られる。まずは、デフォルト値で実行し、結果が思わしくなければオプションを選択ないし変更するという方法を推奨する。
(例)
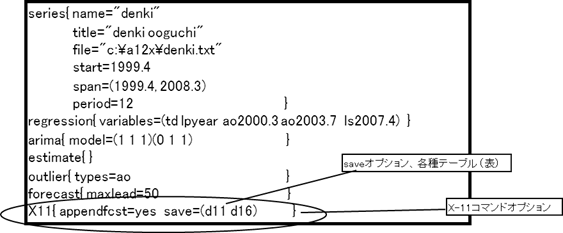
■変動成分の予測値を出力するには、appendfcst=yes、save=d16(条件により、 d10、d12、d13も可能なので確認すること)を指定する。
■季節調整済指数は save=d11 で出力される。
《X-11各種オプション》
|
オプション |
説明 |
オプション内容 |
|
mode 季節調整のタイプ |
乗法型または加法型のモデルを選択。原系列が対数グラフで描かれる時系列の場合は乗法型を、そうでないもの及び0または負のデータを含んでいる時系列の場合は加法型を選択する。 |
mult:乗法型 add:加法型 |
|
seasonalma 移動平均項数 |
季節変動成分を算出するための移動平均の項数を選択。省略時は、MSR(Moving Seasonality Ratio I/S)の値をもとに移動平均項数が自動的に設定される。月、四半期ごとに移動平均項数を分けて指定することも可能。 |
s3*3:加重5項 s3*5:加重7項 s3*9:加重11項 s3*15:加重17項 X11default:旧X11の標準型 |
|
sigmalim 異常値管理限界の上限、下限 |
異常値管理限界(判定基準)の上限および下限を指定。判定基準から異常値として判定された不規則変動成分に偏りの大きさに応じた修正ウェイトをかけて、「異常値調整済不規則変動成分」を算出する。省略時は、上限 2.5、下限1.5が設定される。 |
0以上の数字を指定 (例) x11{sigmalim=(1.8 2.8) } |
|
appendcst 予測結果の収録 |
事前調整済原系列、曜日変動成分、季節変動成分に予測値をつなぎあわせる指定。省略時は予測値なし。 |
(例) x11{appendfcst=yes } |
|
trendma 趨勢循環変動成分の移動平均 |
趨勢循環変動成分をヘンダーソン加重移動平均により算出する際の移動平均項数を指定。省略時には、月次データの場合、通常は 13項移動平均が適用されるが、著しく不規則変動の大きい系列には23項移動平均を、また非常に滑らかな系列については、 9項移動平均が適用される。四半期データの場合は、5項移動平均、または7項移動平均が適用される。 |
1より大きい奇数を設定 (例) x11{trendma=23 } |
《X-11の主なテーブル(表)》 ※saveオプション使用
|
d1 |
事前調整済系列 曜日調整、異常値調整などの事前調整が施された系列。 出力期間は、seriesコマンドのspanオプションで指定した期間。 appendfcst=yesを指定した場合は、forecastコマンドで推計した予測値をつなぎ合わせた期間。 |
|
d10 |
季節変動成分(S) 出力期間は、seriesコマンドのspanオプションで指定した期間。 appendfcst=yesを指定した場合は、forecastコマンドで推計した予測値をつなぎ合わせた期間。(曜日変動成分は含まれない。) |
|
d11 |
季調済系列(TC・I) 出力期間は、seriesコマンドのspanオプションで指定した期間。 (季調済系列の異常値、レベルシフトについて) 異常値、レベルシフトは、事前調整で一旦除去されるが、最終季調済系列には、これらの異常値、レベルシフトが戻される(標準型)。ただし、最終季調済系列から異常値、レベルシフトを除去することも可能( regadjustコマンド、finalオプション)。 |
|
d12 |
趨勢循環変動成分(TC) 出力期間は、seriesコマンドのspanオプションで指定した期間。 趨勢循環変動成分には事前調整で除去したレベルシフトが含まれる。レベルシフトが除去された趨勢循環変動成分は「tal」テーブルを参照のこと。 |
|
d13 |
不規則変動成分(I) 出力期間は、seriesコマンドのspanオプションで指定した期間。 不規則変動成分には事前調整で除去した異常値が含まれる。 |
|
d16 |
季節変動成分+曜日変動成分(S・TD) 出力期間は、seriesコマンドのspanオプションで指定した期間。 apppendfcst=yesを指定した場合は「forecast」コマンドで推計した予測値をつなぎ合わせた期間。 |
|
d18 |
曜日変動成分(TD) 出力期間は、seriesコマンドのspanオプションで指定した期間。 apppendfcst=yesを指定した場合は「forecast」コマンドで推計した予測値をつなぎ合わせた期間。 |
※テーブルの関係(乗法の場合)
原系列=d12 * d13 * d16 (曜日調整をしないときは、d16の代わりにd10でもよい。)
加法の場合は、 原系列=d12+d13+d16 となる。
⇒d11(季節調整済指数)=d12 * d13
⇒原系列/d16 = d12 * d13 = d11(季節調整済指数)
(加法の場合は、積・商を和・差にする。)
3-(7) その他コマンド
■x-12-ARIMAには、上記以外にもコマンドやオプションがあるので、アメリカセンサス局がだしているマニュアルや他の研究者の論文を参考にして、適宜確認して最適なスペックを検討することが望ましい。
(例)
・estimateコマンド・・・
maxiterオプション:ARMA推定(AR、 MAパラメータに対して行う非線形繰り返し推定)における繰り返し回数の許容最大数を指定する。デフォルトは maxiter=200となっている。
≪備考≫
「季節調整法の比較研究」(奥本佳伸)より
以下に、ARIMAモデルの決定方法について奥本氏の論文の概略を紹介する。
奥本氏の考察によると、従来の方法では、AIC値を利用してまず最適なARIMAモデルを決定後に異常値やレベルシフトの検出、回帰変数を検討するが、この場合、最適な ARIMAモデルが変化する場合があることを指摘している。
一方で、異常値等を適用した後にARIMAモデルを再検討するとなると、さらに再度異常値等の再検出を行う必要があり、演算にかかる作業が膨大となる可能性があることも示唆している。
そこで奥本氏は、まずアメリカセンサス局が推薦するARIMAモデル(ARIMA( 0 1 1)(0 1 1))を利用して異常値等を検出し、それを適用後改めてARIMAモデルを決定するという手順を採用した。
1)ARIMA(0 1 1)(0 1 1)を用いて、"outlier"コマンドにより異常値を探索。
2)検出された異常値を変数として加えたうえで、AIC基準によりいくつかの曜日・うるう年調整の変数に応じた最適な ARIMAモデルを選出。
3)モデルと曜日・うるう年調整変数の組み合わせについて係数を推定し、係数が有意でないものはあらかじめ除く。
4)回帰変数の有意性を満たしたケースについてAIC値を計算し、AIC値が最小値となったケースを最終的に採用する。
注意)階差変数が大きいほうがAIC値は低くなる。したがって、階差変数の違うモデル同士を AIC値により比較することはできない。
この方法が最も正確な結果を導くとは限らないが、精度が上がる可能性は十分にあると考えられる。
ARIMAモデルについて
■ARIMAモデルとは・・・季節調整を行う時系列データについて、階差の適用の判断および自己相関、偏自己相関の影響を除去する処理を指定したもの。
 |
![]() ・p…偏自己相関のプロットを参照し、次数1からみて有意な相関がなくなる直近の次数を設定。
・p…偏自己相関のプロットを参照し、次数1からみて有意な相関がなくなる直近の次数を設定。
・d…identifyコマンドにより階差を求める。
・q…自己相関のプロットを参照し、次数1からみて有意な相関がなくなる直近の次数を設定。
・P…偏自己相関のプロットを参照し、12次の整数倍(月次データ)または 4次の整数倍(四半期データ)を次数の低いほうからみて有意な相関が無くなる直近の次数を設定。
・D…identifyコマンドにより階差を求める。
・Q…自己相関のプロットを参照し、12次の整数倍(月次データ)または 4次の整数倍(四半期データ)を次数の低いほうからみて有意な相関が無くなる直近の次数を設定。
■グラフの特徴をつかみ、各パラメータを推測していくつかのモデルを比較する。
実際は、モデルは簡単に判断できないので数種類のモデル数値を検討し、ARIMAモデルに入力してみて、その中で 最もAIC値が小さいものを選択する。( estimateコマンドを利用)
※AIC値とは、モデルのあてはまり度合とパラメータ数を基に算定される値のこと。簡単に言うと、最も安定したグラフ結果を自動的に判定する指数。様々な数値を入力して各結果を比較して、最も値の小さい値を示した結果が最も安定していることを示す。
この数値を用いて、異なる階差同士の結果を比較することはできないので注意すること。
(偏自己相関グラフおよび自己相関グラフとARIMAモデルの対応図)
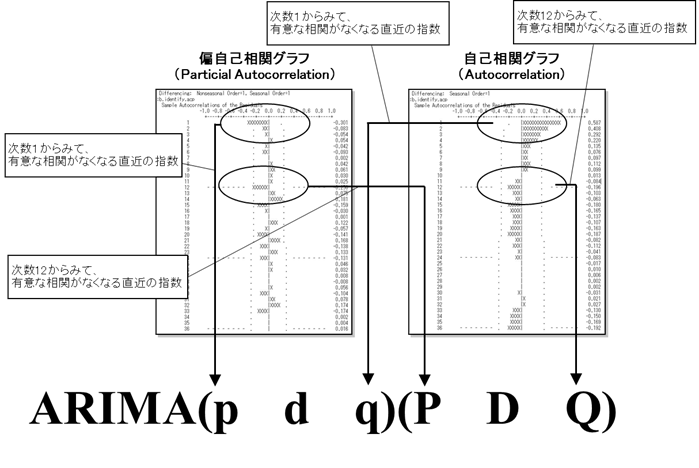
・例えばARIMA(0 1 1)(0 1 1)、ARIMA(1 1 1 )(0 1 1)、ARIMA(2 1 0)(0 1 1) などの形になる。
実際にスペックファイルに入力する際は、
arima{ model=(0 1 1)(0 1 1) }
arima{ model=(1 1 1)(0 1 1) }
arima{ model=(2 1 0)(0 1 1) } といった表記である。